Research
Research in the Numerical Mathematics Group focuses on development of powerful numerical methods and their application to mathematical models. A few current and recent research thrusts are highlighted below.
Structure-preserving discretizations
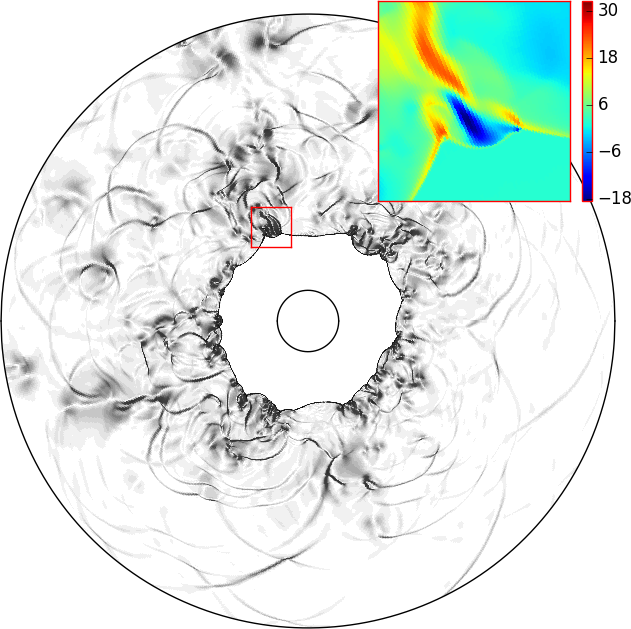
Many mathematical models possess structural properties that characterize their behavior in important qualitative ways. Such properties may include conservation or dissipation of energy, or positivity of values such as density, depth, or concentration. Numerical discretizations that preserve this structure are preferable and often essential. Development of such discretizations can be very challenging. Some of our recent projects along these lines include:
- Enforcing entropy stability to model flow in the kitchen sink
- Enforcing maximum and minimum bounds for scalar transport problems
- Preserving invariants of dispersive nonlinear wave equations
- Relaxation time integrators that preserve an arbitrary functional equality or inequality
Optimization of time integrators
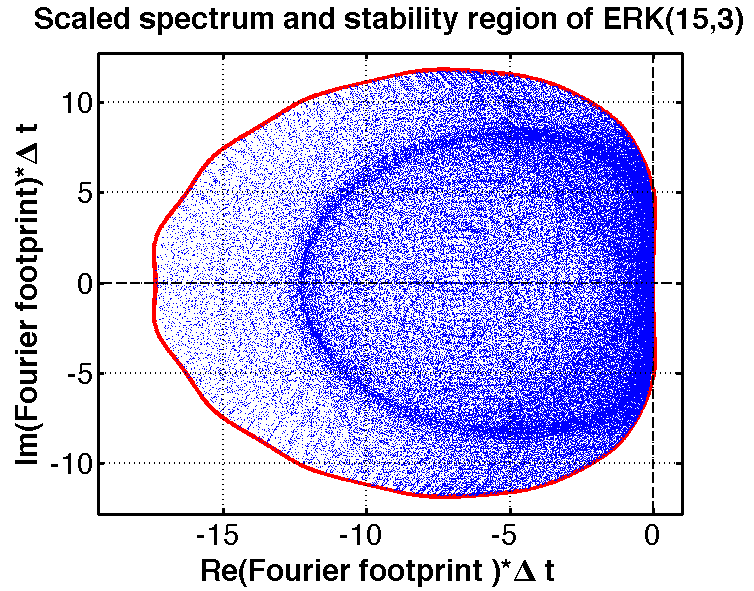
The method of lines is a popular and effective approach to high order accurate solution of time-dependent PDEs. The time integration is typically achieved by use of Runge-Kutta or linear multistep methods. Because of the large number of ODEs involved, this integration is expensive both in terms of computation and memory. Using a time integrator with optimized efficiency and robsustness properties can yield huge dividends. We design such integrators, designing them for properties relevant to specific applications. Such properties include:
- absolute stability regions
- strong stability preservation
- positivity preservation
- accuracy
- efficient time step adaptation
- minimal storage requirements
It is often useful to combine these objectives to design versatile methods.
Nonlinear waves

We apply these powerful numerical methods to discover, characterize, and understand behavior of waves in novel applications. Much of our work in this area focuses on water waves, ranging from flow in the kitchen sink to tsunamis to waves in channels.
Numerical Software and Numerical Analysis Tools
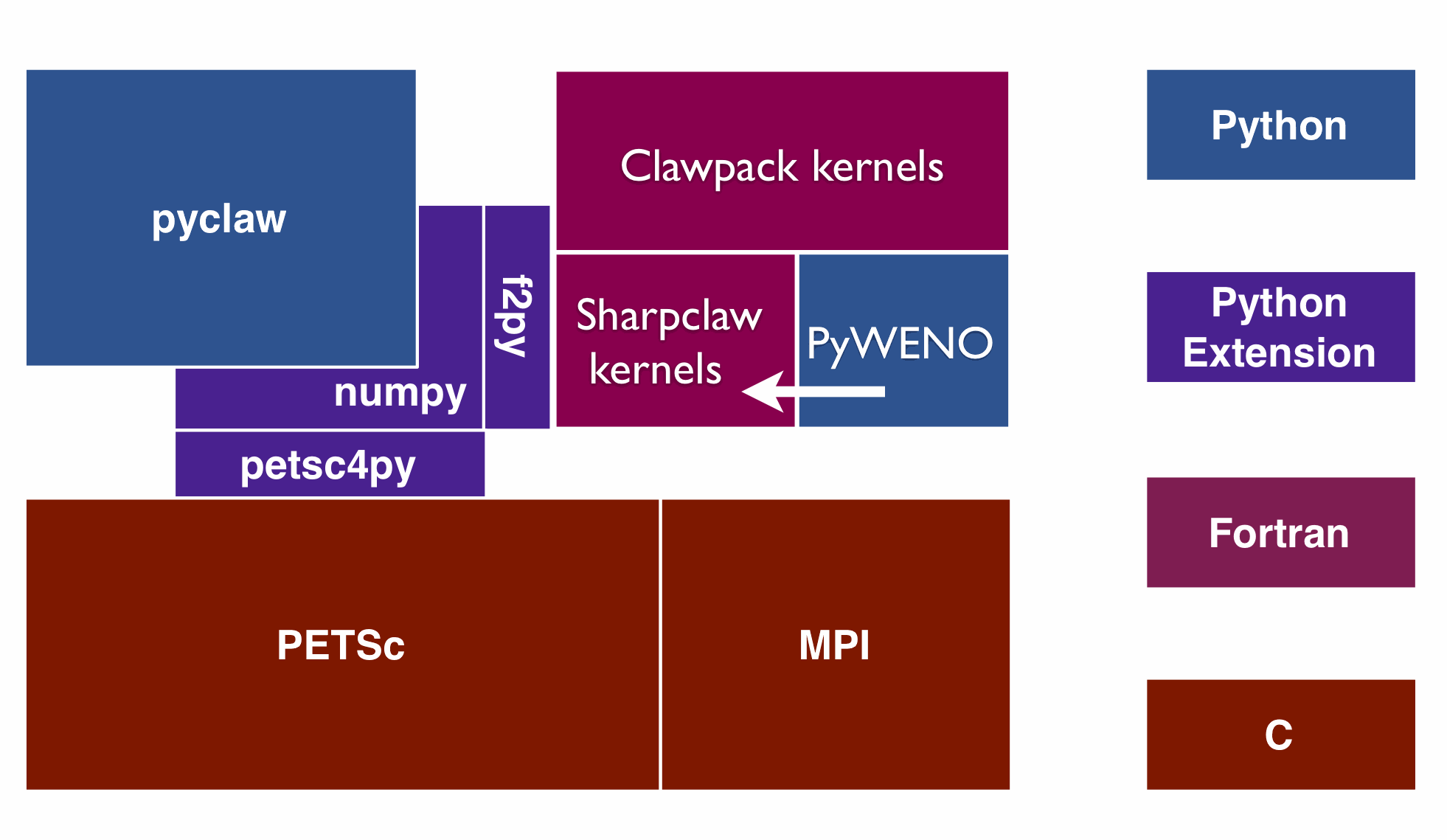
In order for new numerical algorithms to have impact, they must be implemented in software that is both easy to use and powerful enough to solve interesting problems. Computational science software development is an integral part of our research. Additionally, we develop and maintain software whose purpose is to facilitate the design and understanding of numerical methods themselves. For more information, see our software page.